习题课12.06

尹荣洋 $y r y 0204 @ m a i l . u s t c . e d u . c n$

1 作业中的问题

hw 7

第一次 T 3

Answer for HW7

1.3 有心力场

Info

改作业时发现很多同学竟然不会用 $V_{e f f}$ 判断轨道是否有界，这是力学的内容。已知
$E = \frac{1}{2} m {\dot{r}}^{2} + V_{e f f} \Rightarrow 0 = m \dot{r} \frac{d \dot{r}}{d r} + \frac{d V_{e f f}}{d r}$
所以

假设 $\dot{r} > 0$ ，所以朝着物体移动的方向： $r$ 增大的方向，若 $\frac{d V_{e f f}}{d r} > 0$ 也即 $V_{e f f}$ 增加就意味着 $\frac{d \dot{r}}{d r} < 0$ ，即速度减小，粒子被束缚。
假设 $\dot{r} < 0$ ，所以朝着物体移动的方向： $r$ 减小的方向，若 $\frac{d V_{e f f}}{d (- r)} > 0 o r \frac{d V_{e f f}}{d r} < 0$ 也即 $V_{e f f}$ 增加就意味着 $\frac{d \dot{r}}{d r} > 0 o r \frac{d \dot{r}}{d (- r)} > 0$ ，即速度减小，粒子被束缚。

上述的情形对应如下图片当中 $E_{1} < E < E_{2}, r_{1} < r < r_{2}$ 的片段：
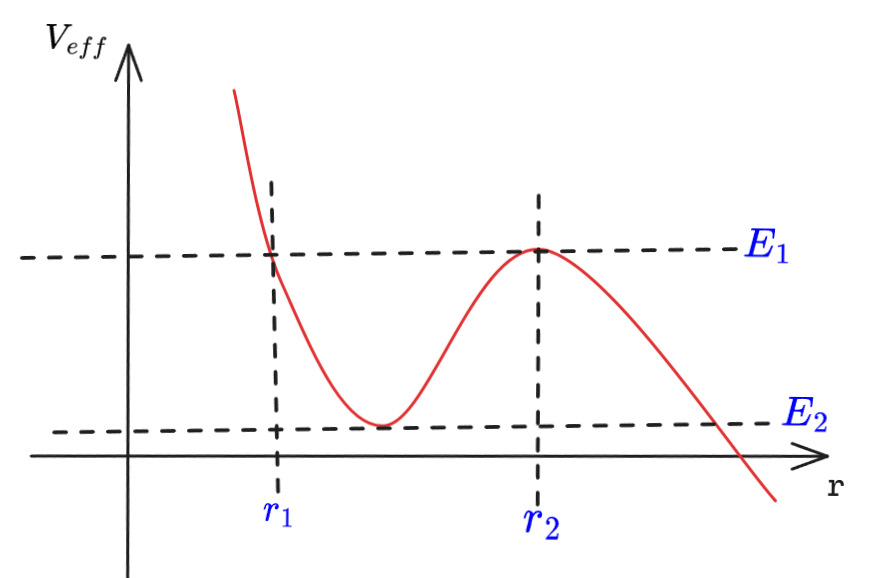
zz_figure/Pasted image 20251115144621.png

画一条水平线，它的纵坐标为 $E$ ，因为 $E = \frac{1}{2} m {\dot{r}}^{2} + V_{e f f}$ ，所以若此时 $V_{e f f}$ 曲线在该水平线下侧，那么水平线与 $V_{e f f}$ 曲线的差距就是径向动能 $\frac{1}{2} m {\dot{r}}^{2}$ ，所以若初始时轨道在 $E_{1} < E < E_{2}, r_{1} < r < r_{2}$ 的片段，那么运动就无法跨过区间两侧的势垒，否则 $\frac{1}{2} m {\dot{r}}^{2} < 0$ ，物体被束缚。

若刚好 $E = E_{2}$ ，那么物体就只能待在极小值点，也就是做圆轨道运动。若 $E > E_{1}$ 并且从 $r < r_{1}$ 开始运动，那么就可以轻而易举地跨越势垒，导致运动无界。若 $E < E_{1}$ ，但物体没有运动到被束缚的区间 $r_{1} < r < r_{2}$ ，而是运动在 $r > r_{2}$ ，那么朝着 $r$ 增大的方向，径向动能 $\frac{1}{2} m {\dot{r}}^{2}$ 越大，轨道也是无界的。开普勒运动中，就是这样来区分三种轨道的。

(a) 线性力 $\vec{F} = - k \vec{r}$ , $U = \frac{1}{2} k r^{2}$

因为切换大小写过于麻烦，所以以下讨论用 $h$ 代替 $L$ ，约化质量 $μ$ 代替 $m$ .

我们使用 binet 微商方程，做如下换元：
$u \equiv \frac{1}{r^{2}}$
那么
$\frac{d u}{d ϕ} = - \frac{2}{r^{3}} \frac{d r}{d ϕ}$
$\dot{r} = \frac{d r}{d ϕ} \dot{ϕ} = - \frac{r^{3}}{2} \dot{ϕ} \frac{d u}{d ϕ} = - \frac{r}{2} \frac{h}{μ} \frac{d u}{d ϕ}$
同时能量守恒给出：
$\frac{1}{2} μ {\dot{r}}^{2} = \frac{1}{8} \frac{h^{2}}{u μ} (\frac{d u}{d ϕ}) = E - \frac{h^{2}}{2 μ} u - \frac{k}{2 u}$
整理第二个等号得到：
${(\frac{d u}{d ϕ})}^{2} + 4 u^{2} - \frac{8 E μ}{h^{2}} u = - \frac{4 k μ}{h^{2}}$
改写为：
${[\frac{d}{d ϕ} (u - \frac{E μ}{h^{2}})]}^{2} + 4 {(u - \frac{E μ}{h^{2}})}^{2} = - \frac{4 k μ}{h^{2}} + 4 (\frac{E μ}{h^{2}})$
该方程可分离变量求解，得到：
$u = \frac{E μ}{h^{2}} + \frac{E μ}{h^{2}} {(1 - \frac{k h^{2}}{E^{2} μ})}^{1 / 2} \cos 2 (ϕ - ϕ_{0}) \equiv \frac{1}{r^{2}}$
做换元 $(x, y) = r (\cos ϕ, \sin ϕ)$ 并取 $ϕ_{0} = 0$ 可发现上式为圆锥曲线方程，其离心率满足：
${(1 - \frac{k h^{2}}{E^{2} μ})}^{1 / 2} = \frac{e^{2}}{2 - e^{2}}$
离心率 $e$ ，或者说 $k$ 的正负(排斥或吸引势)，将确定轨道的形状。注意 $e$ 不但大于 $0$ ，还要小于 $\sqrt{2}$ （因为上式为平方根，要大于 0）。

此外，本题选用拉格朗日方程的方法可更快得到结果。（采用直角坐标，发现拉格朗日方程就是简谐振动方程）

(b) 球方势阱 $V (r) = - V_{1} (r < a), V (r) = 0 (r > a)$

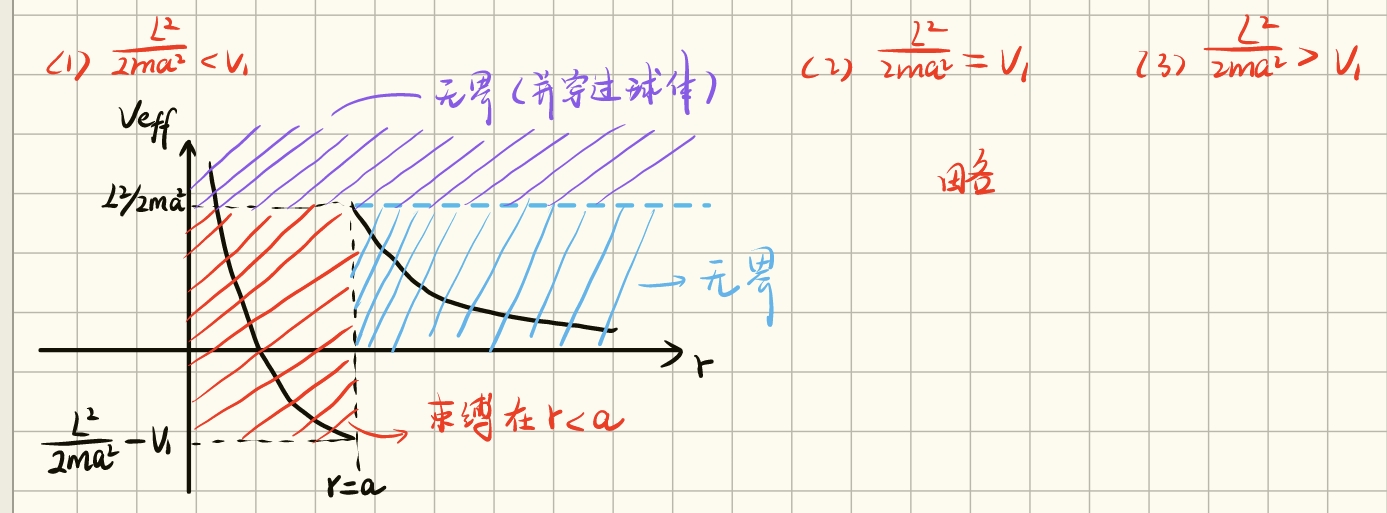
假设 $V_{1} > 0$ 。如果物体的瞄准距离 $d$ 大于 $a$ , 显然只会(1)在球外做直线运动，反之，轨道(2)在球内发生折射或者(3)被束缚在球内。

一般来说，可以分三种情形绘制如下 $V_{e f f}$ ，以此确定轨道的有界还是无界，注意对于球外的物体，穿过球体的条件 $d < a$ 等价于 $E = \frac{1}{2} m v_{\infty}^{2} > \frac{L^{2}}{2 m a^{2}}$ （对应于下图紫色区域，即 $E > \frac{L^{2}}{2 m a^{2}}, 存在 r < a$ ）

zz_figure/Capture_20251115_140716.jpg

(c) 反比力

见 HW6的T2，根据 $E$ 和 $\frac{h^{2}}{2 μ} - k$ 的正负可确定轨道形状。通过 $V_{e f f}$ 作图可以进一步确认轨道是否有界。

(d) Yukawa 势 $U (r) = - \frac{k e^{- α r}}{r}$

对于 $V_{e f f} (r) = \frac{h^{2}}{2 μ r^{2}} - \frac{k e^{- α r}}{r}$ ，有
$\frac{d V_{e f f}}{d r} = - \frac{h^{2}}{μ r^{3}} + k e^{- α r} \frac{α r + 1}{r^{2}} = r^{- 3} f (r), f (r) = k e^{- α r} (α r + 1) r - \frac{h^{2}}{μ}$
令 $\frac{d V_{e f f}}{d r} = 0$ , 可以得到对应圆轨道的半径，在常见情形下( $k > 0, α > 0$ )，该方程有 0~2 个根（对应 $V_{e f f}$ 有 0~2 个极值点）。据此可以画出 $V_{e f f} (r)$ 的图像，根据直线 $V_{e f f} = E$ 在途中的位置，可以将轨道分为几种类型：

无界(类似抛物线/双曲线但与之偏离。或者从无穷远入射，环绕几圈后再返回无穷远);
进动(类椭圆轨道的进动);
圆(特殊情形，但处于势能极大时容易不稳定)。

所以根据 $\frac{d V_{e f f}}{d r} = 0$ 根的个数得到如下图：

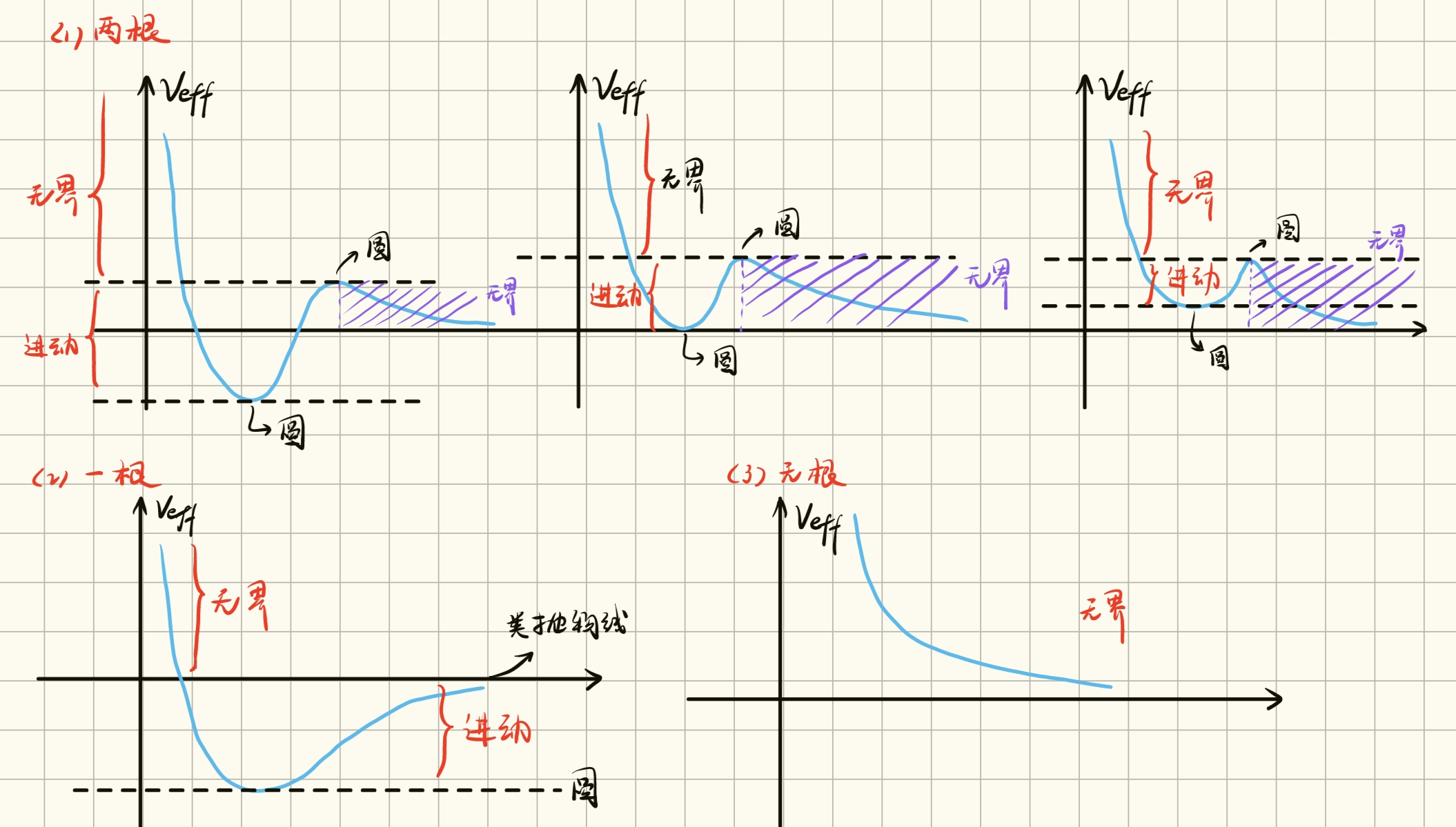
zz_figure/Capture_20251115_141631.jpg

对于最常见的第一种情形， $f (r)$ 在 $[0, + \infty)$ 区间上被 $V_{e f f}$ 的两个极值点 $r_{1}, r_{2}$ 分割，符号变化为 $- \to + \to -$ ， $f (r)$ 的极大值点由 $f^{'} (r_{0}) = 0$ 得到, 为 $r_{0} = \frac{1 + \sqrt{5}}{2 α}$ ，由上述几个曲线可知，要使得轨道有界，必须存在 $\frac{d V_{e f f}}{d r} = 0$ 或者说存在 $f (r_{1, 2}) = 0$ 成立，那么必须有
$f (r_{0}) > 0$
于是得到
$α \frac{h^{2}}{μ} < 2 (2 + \sqrt{5}) k e^{- (\sqrt{5} + 1) / 2}$
若上式不成立，则轨道无界。反之，三种情况都有可能。

hw 8 振动

久期方程的线代原理： $A_{n \times n} x = 0$ 有非平凡解的条件： $d e t (A) = 0$ 或者说 $r a n k (A) < n$ ， $n - r a n k (A)$ 为解空间的维数/解的自由度。
最后的结果不要包含一堆自设的符号，看不懂

hw 9

缺少齐次通解(初态解)。为满足意义，最终解要取实部。

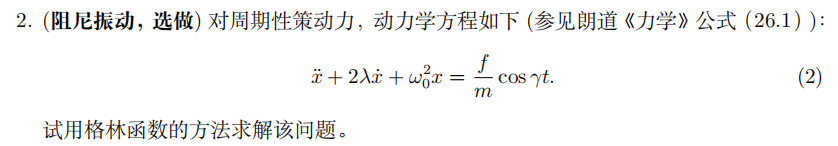
格林函数，没学过数学物理方法和复变不建议写，写了也没什么用

2 一些 tips

怎么记忆几类正则变换

往年一般是闭卷考，生成函数的公式不会给。

记忆生成函数的自变量：
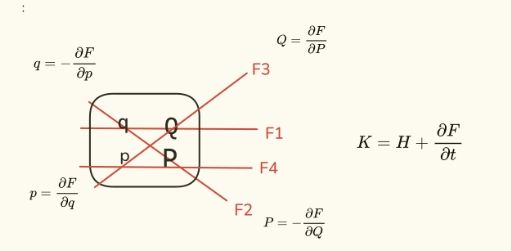
记忆生成函数的偏导关系

$δ F$ 无非由以下几项构成：

p δ q, Q δ P, - q δ p, - P δ Q

只需要记住前两个，后两个带负号。于是 1~4 类变换对号入座即可。

如果实在不想记，可以只记 $F_{2}$ ，前两年都考的第二类，当然今年不确定（我也不敢说绝对）。

怎么证明一个变换是正则变换

有三种方法，最简单也最方便的一种是：保泊松括号/辛结构的变换是正则变换，即只需证明

[Q_{j}, P_{i}] = δ_{i j} o r [ξ_{i}, ξ_{j}] = ω_{i j}

$ω_{2 s \times 2 s} = [\begin{matrix} 0_{s \times s} & I_{s \times s} \\ - I_{s \times s} & 0_{s \times s} \end{matrix}]$ 是单位矩阵 $I$ 的辛形式， $ξ_{α} = (q_{1}, q_{2} \dots, q_{s}, p_{1}, p_{2} \dots, p_{s})^{T}$ 是相空间变量的辛形式。

做题基本上只用到上式的一个等式，下面两种方法通常用不到(不好用)。第二种方法(教材的方法)，以下变分是全微分

p_{α} δ q - P δ Q = δ F_{1} (Q, q, t)

这个全微分也可以选取其他三类生成函数。

第三种方法，保辛的变换是正则变换

M ω M^{T} = ω

对于变换 $ξ \to ξ^{'}$ ， $M_{α β} = \frac{\partial ξ_{β}^{'}}{\partial ξ_{α}}$ 是变换矩阵的辛形式。你可以把正则变换想象成在相空间做“旋转”，类似在欧式空间的正交变换(即 $R I R^{T} = I$ ，参见高显讲义)。

存在某类正则变换需要什么条件

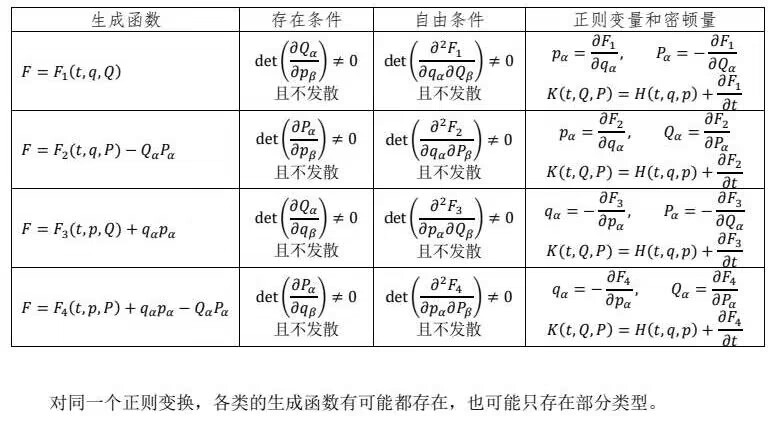
自由条件保证变换可逆/非退化，存在条件保证变量之间的独立性。

3 欧式空间的矢量和张量运算

三维欧几里得空间中，只用下角标来表示张量(分量)，如应力张量 $P_{i j}$ ，它是一个二阶张量。

闵氏空间(狭相)和黎曼空间(广相)不在本文的考虑范围内。

3.1 基本约定

爱因斯坦求和约定：除非特殊说明，否则默认对出现两次的相同指标求和，如 $\vec{x} = x_{i} {\vec{e}}_{i} = x_{1} {\vec{e}}_{1} + x_{2} {\vec{e}}_{2} + x_{3} {\vec{e}}_{3}$ . 偶尔出于某种特殊需要, 相同的指标可能出现三次及以上, 此时也默认求和.
单位正交坐标基矢： ${\vec{e}}_{i}$
单位并矢： ${\vec{e}}_{i} {\vec{e}}_{j}$ 。比如一个二阶 $3 \times 3$ 的矩阵，可以把 ${\vec{e}}_{i} {\vec{e}}_{j}$ 理解为第 $i$ 行 $j$ 列为 $1$ ,其他元素均为 $0$ 的矩阵，或者理解为列向量 $e_{i}$ 与行向量 $e_{j}^{T}$ 的矩阵乘积，或者理解为二阶张量的一个“基”张量（类似于基向量）。类似的可以把更多基矢并在一起，表示更高阶的张量分量。
二阶 $k r o n e c k e r 符号$ ： $δ_{i j} = e_{i} \cdot e_{j} \overset{△}{=} I_{i j} (单位矩阵)$

令 $e_{i} \times e_{j} = ϵ_{i j k} e_{k}$ 得到：

三阶 $L e v i - C i v i t a$ 符号：

ϵ_{i j k} = {\begin{matrix} + 1 当 i, j, k 为 偶 排 列 \\ - 1 当 i, j, k 为 奇 排 列 \\ 0 当 存 在 相 同 指 标 \end{matrix}

可以简单地在 $x y z$ 坐标系用右手螺旋验证上述定义的正确性。

直角坐标系下，梯度 $\nabla f = {\vec{e}}_{i} \frac{\partial f}{\partial x_{i}} \overset{简记为}{=} {\vec{e}}_{i} \partial_{i} f$

所以简记 $n a b l a$ 算子为 : $\nabla = g r a d = \frac{\partial}{\partial \vec{r}} = {\vec{e}}_{i} \partial_{i}$

3.2 已知关系的角标形式

利用上述约定，有：

矢量展开 $\vec{a} = a_{i} {\vec{e}}_{i}$
点乘 $\vec{a} \cdot \vec{b} = a_{i} {\vec{e}}_{i} \cdot b_{j} {\vec{e}}_{j} = a_{i} b_{j} δ_{i j} = a_{i} b_{i}$
叉乘 $\vec{a} \times \vec{b} = a_{i} {\vec{e}}_{i} \times b_{j} {\vec{e}}_{j} = ϵ_{i j k} a_{i} b_{j} {\vec{e}}_{k} \to (\vec{a} \times \vec{b})_{k} = a_{i} {\vec{e}}_{i} \times b_{j} {\vec{e}}_{j} = ϵ_{i j k} a_{i} b_{j}$
张量展开 $\vec{\vec{A}} = A_{i j} {\vec{e}}_{i} {\vec{e}}_{j}$
$L a p l a c e$ 算符 $Δ = \nabla^{2} = \nabla \cdot \nabla = e_{i} \partial_{i} \cdot e_{j} \partial_{j} = δ_{i j} \partial_{i j} = \partial_{i}^{2}$
散度 $d i v \vec{v} = e_{i} \partial_{i} \cdot v_{j} e_{j} = \partial_{i} v_{i}$
旋度 $r o t \vec{v} = e_{i} \partial_{i} \times v_{j} e_{j} = ϵ_{i j k} \partial_{i} v_{j}$
此外，还有一个即将用到的等式 $ϵ_{i j k} ϵ_{i m n} = δ_{j m} δ_{k n} - δ_{j n} δ_{k m}$

证明它很简单，只需要分别讨论 $(1) j = m, k = n$ 和 $(2) j = n, k = m$ 两种情况。口诀：先对齐再交叉。

更一般地

$ϵ_{i j k} ϵ_{l m n} = det (\begin{matrix} δ_{i l} & δ_{i m} & δ_{i n} \\ δ_{j l} & δ_{j m} & δ_{j n} \\ δ_{k l} & δ_{k m} & δ_{k n} \end{matrix})$

高维情形：

ϵ_{i_{1} i_{2} \dots i_{n}} ϵ_{j_{1} j_{2} \dots j_{n}} = det (\begin{matrix} δ_{i_{1} j_{1}} & δ_{i_{1} j_{2}} & \dots & δ_{i_{1} j_{n}} \\ δ_{i_{2} j_{1}} & δ_{i_{2} j_{2}} & \dots & δ_{i_{2} j_{n}} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ δ_{i_{n} j_{1}} & δ_{i_{n} j_{2}} & \dots & δ_{i_{n} j_{n}} \end{matrix})

3.3 矢量运算的基本公式

本节略去小写字母头上的矢量箭头。

三重积轮换（平行六面体体积）：
$a \cdot (b \times c) = b \cdot (c \times a) = c \cdot (a \times b)$

证明：
$a \cdot (b \times c) = a_{k} (b \times c)_{k} = a_{k} b_{i} c_{j} ϵ_{i j k} = b_{i} (c_{j} a_{k} ϵ_{j k i}) = b_{i} (c \times a)_{i} = b \cdot (c \times a)$

三叉乘：
$a \times (b \times c) = b (a \cdot c) - c (a \cdot b) o r (b \times c) \times a = c (a \cdot b) - b (a \cdot c)$

口诀：先中间再外边

证明：

\begin{array}{l} a \times (b \times c) & = ϵ_{i j k} a_{i} (b \times c)_{j} e_{k} \\ = ϵ_{i j k} a_{i} ϵ_{m n j} b_{m} c_{n} e_{k} \\ = e_{k} ϵ_{j k i} ϵ_{j m n} a_{i} b_{m} c_{n} \\ = (δ_{k m} δ_{i n} - δ_{k n} δ_{i m}) e_{k} a_{i} b_{m} c_{n} \\ = e_{m} b_{m} a_{n} c_{n} - e_{n} c_{n} a_{m} b_{m} \\ = b (a \cdot c) - c (a \cdot b) \end{array}

叉乘的点乘

(a \times b) \cdot (c \times d) = (a \cdot c) (b \cdot d) - (a \cdot d) (b \cdot c)

或者利用三重积轮换得到：

(a \times b) \cdot (c \times d) = a \cdot [b \times (c \times d)] = c \cdot [d \times (a \times b)]

或者利用三叉乘得到：

a \cdot [b \times (c \times d)] = (a \cdot c) (b \cdot d) - (a \cdot d) (b \cdot c)

更复杂的公式完全可以类似操作。

3.4 $\nabla$ 的基本运算

梯度场无旋： $\nabla \times \nabla f = 0$

证明：
$左侧 = ϵ_{i j k} \partial_{i} (\nabla f)_{j} e_{k} = ϵ_{i j k} \partial_{i} \partial_{j} f e_{k} = - ϵ_{j i k} \partial_{j} \partial_{i} f e_{k}$ ，默认偏导可以换序，可见对于同一个 $e_{k}$ 项， $i$ 和 $j$ 互换的两项相消，结果 $= 0$ .

旋度场无散： $\nabla \cdot \nabla \times \vec{A} = 0$

证明：
$左侧 = \partial_{k} (\nabla \times \vec{A})_{k} = ϵ_{i j k} \partial_{k} \partial_{i} A_{j}$ ，你会发现 $i$ 和 $k$ 互换的两项也相消。

类似于函数乘积的微分：

$\nabla f g = f \nabla g + g \nabla f$
$\nabla \cdot (f \vec{A}) = f \nabla \cdot \vec{A} + \vec{A} \cdot \nabla f$
$\nabla \times (f \vec{A}) = f \nabla \times \vec{A} + \nabla f \times \vec{A}$

类似之前的证明，比如证明（3）式:
$左侧 = ϵ_{i j k} \partial_{i} (f A_{j}) e_{k} = f ϵ_{i j k} (\partial_{i} A_{j}) e_{k} + A_{j} ϵ_{i j k} (\partial_{i} f) e_{k} = 右侧$

叉乘的散度： $\nabla \cdot (\vec{A} \times \vec{B}) = \vec{B} \cdot \nabla \times \vec{A} - \vec{A} \cdot \nabla \times \vec{B}$
叉乘的旋度： $\nabla \times (\vec{A} \times \vec{B}) = (\vec{B} \cdot \nabla) \vec{A} + (\nabla \cdot \vec{B}) \vec{A} - (\vec{A} \cdot \nabla) \vec{B} - (\nabla \cdot \vec{A}) \vec{B}$
点乘的梯度： $\nabla (\vec{A} \cdot \vec{B}) = \vec{A} \times (\nabla \times \vec{B}) + \vec{B} \times (\nabla \times \vec{A}) + (\vec{A} \cdot \nabla) \vec{B} + (\vec{B} \cdot \nabla) \vec{A}$

上面没有给证明的几个公式虽说也能用已经提到的方法证明，但还是下面的费曼法更简单：

3.5 $\nabla$ 的费曼法分解

已知， $\nabla = {\vec{e}}_{i} \partial_{i}$ ，费曼把 $\nabla$ 的矢量属性 $e_{i}$ 和微分属性 $\partial_{i}$ 分离开来，让计算变得简单。只需把作用于张量 A 的 $\nabla$ 算子记作 $\nabla_{A}$ ，然后当作矢量进行计算，最后把作用不同张量的 $\nabla$ 算子合并，就能得到结果，举个栗子：

证明上述提到的点乘的梯度： $\nabla (\vec{A} \cdot \vec{B}) = \vec{A} \times (\nabla \times \vec{B}) + \vec{B} \times (\nabla \times \vec{A}) + (\vec{A} \cdot \nabla) \vec{B} + (\vec{B} \cdot \nabla) \vec{A}$

拆分： $\nabla (A \cdot B) = \nabla_{A} (A \cdot B) + \nabla_{B} (B \cdot A)$

\begin{matrix} B \times (C \times A) = C (A \cdot B) - A (C \cdot B) \\ \overset{C \to \nabla_{A}}{\Rightarrow} B \times (\nabla_{A} \times A) = \nabla_{A} (A \cdot B) - A (\nabla_{A} \cdot B) \\ \Rightarrow \nabla_{A} (A \cdot B) = B \times (\nabla_{A} \times A) + A (\nabla_{A} \cdot B) = B \times (\nabla_{A} \times A) + (B \cdot \nabla_{A}) A \end{matrix}

最后一步进行了换序： $A (\nabla_{A} \cdot B) = (B \cdot \nabla_{A}) A$ ，因为 $\nabla_{A}$ 必须作用于 A 上。

同理： $\nabla_{B} (B \cdot A) = A \times (\nabla_{B} \times B) + (A \cdot \nabla_{B}) B$

于是： $\nabla (A \cdot B) = \nabla_{A} (A \cdot B) + \nabla_{B} (B \cdot A) = B \times (\nabla_{A} \times A) + (B \cdot \nabla_{A}) A + A \times (\nabla_{B} \times B) + (A \cdot \nabla_{B}) B$

$n a b l a$ 算子合并后： $\nabla (A \cdot B) = B \times (\nabla \times A) + (B \cdot \nabla) A + A \times (\nabla \times B) + (A \cdot \nabla) B$

此外，还有一个有用的结论，与上式相似但区别： $\nabla A^{2} = \nabla (A \cdot A) = \vec{\nabla} \vec{A} \cdot 2 \vec{A}$ ，标上矢量记号是为了突出这是一个矢量和二阶张量的点乘，结果自然是矢量。

证明：

左侧 $= \partial_{i} (A_{j} A_{j}) {\vec{e}}_{i} = 2 A_{j} \partial_{i} A_{j} {\vec{e}}_{i} = \partial_{i} A_{j} {\vec{e}}_{i} 2 A_{k} δ_{j k} = \partial_{i} A_{j} {\vec{e}}_{i} {\vec{e}}_{j} \cdot 2 A_{k} {\vec{e}}_{k}$

注意 $2 \vec{A}$ 一定是 $右乘$ 在 $\vec{\nabla} \vec{A}$ 上，即 $上述证明中 e_{k} 作用在 e_{j} 而不是 e_{i} 上。$

我不知道费曼是如何一拍脑袋想到这个方法的，事实证明这个方法偶尔会出些问题——为避免它们，最好保证公式左侧的 $\nabla$ 能够作用于所有矢量&张量，以便其矢量属性和微分属性能够“良好地”分离，反例是，对于 $B \times (\nabla \times A)$ 这种形式则尽量不要用费曼法，因为可以看到， $\nabla$ 的矢量属性作用于 B，而微分属性不会作用于 B，那到底要不要保留 $\nabla_{B}$ ？其实保不保留都是错的，它的结果是(从点乘的梯度得到)： $\nabla (A \cdot B) - [(B \cdot \nabla) A + A \times (\nabla \times B) + (A \cdot \nabla) B]$ ，读者可以自行验证。

3.6 $\nabla$ 在曲线正交坐标系的表示

只考虑正交坐标系(即, 坐标轴两两正交)。

3.6.1 拉梅系数

（不严格）定义拉梅系数 $h_{i}$ ：满足线段微元 $d s^{2} = h_{i}^{2} d r_{i}^{2}$ ，比如笛卡尔坐标系下 $d s^{2} = d x^{2} + d y^{2} + d z^{2}$ , 亦笛卡尔坐标的三个拉梅系数均为 $1$ 。不难看出，柱坐标和球坐标的拉梅系数如下：

柱坐标
$h_{r}$	1
$h_{θ}$	$r$
$h_{z}$	1

球坐标
$h_{r}$	$1$
$h_{θ}$	$r$
$h_{φ}$	$r s i n θ$

一个结论是， $h_{1} h_{2} h_{3}$ 正是雅可比行列式的值（淑芬 B 2：三重积分），简记为 $J$ 。

3.6.2 $\nabla$ 的一般表示

在曲线正交坐标系下, $\nabla$ 的形式发生了一些变化. 这里依旧以梯度作为出发点 :

1) 梯度.

拉梅系数的定义的另一种写法为：

h_{i} = | \frac{\partial \vec{r}}{\partial r_{i}} |

其中 $\vec{r}$ 是位置矢量, $\vec{r} = r_{i} {\vec{e}}_{i}$ , 其微分形式为：

d \vec{r} = h_{i} {\vec{e}}_{i} d r_{i}

注意上式中多出的拉梅系数 $h_{i}$ (比如极坐标的圆弧 $d l = r d θ$ , $r$ 就是那个多出来的拉梅系数). 另外, 在任意坐标系中，梯度算符的定义应满足：

\nabla f \cdot d \vec{r} = d f = \frac{\partial f}{\partial r_{i}} d r_{i}

假设 $\nabla f$ 表示为：

\nabla f = A_{i} {\vec{e}}_{i}

代入上式得到：

A_{i} {\vec{e}}_{i} \cdot h_{j} {\vec{e}}_{j} d r_{j} = A_{i} h_{i} d r_{i} = \frac{\partial f}{\partial r_{i}} d r_{i} \Rightarrow A_{i} = \frac{1}{h_{i}} \frac{\partial f}{\partial r_{i}}

因此根据爱因斯坦求和约定，梯度算符可以简写为：

\nabla = \frac{1}{h_{i}} {\vec{e}}_{i} \partial_{i}

利用拉梅系数, 容易有如下结论:

弧微元: $d s_{i} = h_{i} d r_{i}$ (不求和)
弧长微元: $d s^{2} = h_{i}^{2} d r_{i}^{2}$
面微元: $d s_{i} d s_{j} = h_{i} h_{j} d r_{i} d r_{j}$ (不求和)
体积微元: $d V = h_{1} h_{2} h_{3} d r_{1} d r_{2} d r_{3} = | J | d r_{1} d r_{2} d r_{3}$

下面继续推导散度, 旋度, 以及 $\nabla^{2}$ 的形式. 需要提前注意的是矢量和张量不随坐标系的选取而变化, $\nabla$ 也是类似的(只要不将它展开成分量形式), 也就是说, 类似于 $\nabla \cdot (f \vec{A}) = f \nabla \cdot \vec{A} + \vec{A} \cdot \nabla f$ 的前面提到在直角坐标系中成立的公式, 换到正交曲线坐标依旧成立, 不一样的只是它的展开分量变了.

2) 散度.

引理 : $\nabla \cdot (\frac{\vec{e_{1}}}{h_{2} h_{3}}) = \nabla \cdot (\frac{\vec{e_{2}}}{h_{3} h_{1}}) = \nabla \cdot (\frac{\vec{e_{3}}}{h_{1} h_{2}}) = 0$ , 注意到三个方向平权(谁也不比谁优越), 所以只需要证 $\nabla \cdot (\frac{\vec{e_{1}}}{h_{2} h_{3}}) = 0$ 即可.

证明 :

∵ \nabla = \frac{1}{h_{i}} {\vec{e}}_{i} \partial_{i} \Rightarrow \nabla r_{1} = \frac{{\vec{e}}_{1}}{h_{1}}

\begin{matrix} \nabla \times \nabla v = 0 \Rightarrow \nabla \times (\frac{{\vec{e}}_{1}}{h_{1}}) = \nabla \times (\nabla r_{1}) = 0 \Rightarrow \nabla \times (\frac{{\vec{e}}_{i}}{h_{i}}) = 0 \\ \nabla \cdot (\frac{\vec{e_{1}}}{h_{2} h_{3}}) = \nabla \cdot (\frac{\vec{e_{2}}}{h_{2}} \times \frac{\vec{e_{3}}}{h_{3}}) \overset{\nabla \cdot (\vec{A} \times \vec{B}) = \vec{B} \cdot \nabla \times \vec{A} - \vec{A} \cdot \nabla \times \vec{B}}{=} \nabla \times (\frac{\vec{e_{2}}}{h_{2}}) \cdot \frac{\vec{e_{3}}}{h_{3}} - \nabla \times (\frac{\vec{e_{3}}}{h_{3}}) \cdot \frac{\vec{e_{2}}}{h_{2}} = 0 证 毕 . \end{matrix}

接下来尝试将散度展开 :

\begin{array}{l} \nabla \cdot \vec{v} & = \nabla \cdot v_{k} {\vec{e}}_{k} \\ = \nabla \cdot (h_{i} h_{j} v_{k}) \frac{\vec{e_{k}}}{h_{i} h_{j}} (i, j, k 互 不 相 同, 对 k 求 和) \end{array}

使用 $\nabla \cdot (f \vec{A}) = f \nabla \cdot \vec{A} + \vec{A} \nabla f$ :

\nabla \cdot \vec{v} = h_{i} h_{j} v_{k} \nabla \cdot \frac{\vec{e_{k}}}{h_{i} h_{j}} + \frac{\vec{e_{k}}}{h_{i} h_{j}} \cdot \nabla (h_{i} h_{j} v_{k})

第一项根据引理为 $0$ , 第二项正常地把 $\nabla$ 展开并保留 ${\vec{e}}_{k}$ 项即可得到 :

\nabla \cdot \vec{v} = \frac{1}{h_{i} h_{j} h_{k}} \partial_{k} (h_{i} h_{j} v_{k}) = \frac{1}{| J |} \partial_{k} (h_{i} h_{j} v_{k}) (i, j, k 互 不 相 同, 对 k 求 和)

3) 旋度.

先给出结果 :

\nabla \times \vec{v} = \frac{1}{| J |} | \begin{matrix} h_{1} {\vec{e}}_{1} & h_{2} {\vec{e}}_{2} & h_{3} {\vec{e}}_{3} \\ \partial_{1} & \partial_{2} & \partial_{3} \\ h_{1} v_{1} & h_{2} v_{2} & h_{3} v_{3} \end{matrix} |

Drawing 2024-12-17 22.53.10.excalidraw

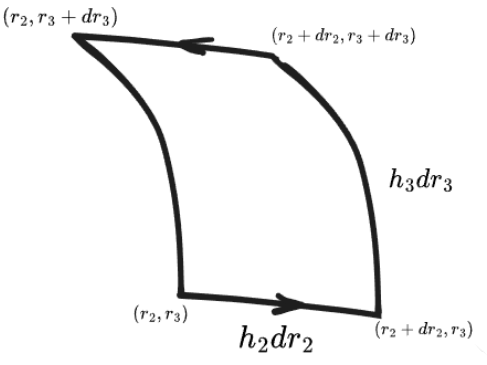
$\vec{n} (S)$ 为某个面元 $Δ S$ 的正方向, 以环量定义旋度在 $\vec{n} (S)$ 方向的分量为 $\vec{n} (S) \cdot \nabla \times \vec{v} = lim_{Δ S \to 0} \frac{\oint_{\partial S} \vec{v} \cdot d \vec{r}}{Δ S}$ , 不妨取 $\vec{n} (S)$ 为 ${\vec{e}}_{1}$ , 于是积分环路变为上图, 即 :

\begin{array}{l} (\nabla \times \vec{v})_{1} & = lim_{d r \to 0} \frac{(v_{2} h_{2} |_{r_{3}} d r_{2} - v_{2} h_{2} |_{r_{3} + d r_{3}} d r_{2}) + (v_{3} h_{3} |_{r_{2} + d r_{2}} d r_{3} - v_{3} h_{3} |_{r_{2}} d r_{3})}{h_{2} h_{3} d r_{2} d r_{3}} \\ = lim_{d r \to 0} \frac{- \partial_{3} (v_{2} h_{2}) d r_{3} d r_{2} + \partial_{2} (v_{3} h_{3}) d r_{2} d r_{3}}{h_{2} h_{3} d r_{2} d r_{3}} \\ = \frac{h_{1}}{h_{1} h_{2} h_{3}} (\partial_{2} (h_{3} v_{3}) - \partial_{3} (h_{2} v_{2})) \end{array}

满足一开始给出的旋度结果的第一个分量. 其他两个分量也可以类似证明.

4) $l a p l a c e$ 算符.

这里不需要再引入新的东西, 直接得到:

\nabla^{2} v = \nabla \cdot \nabla v = \frac{1}{| J |} \partial_{k} (h_{i} h_{j} (\nabla v)_{k}) = \frac{1}{| J |} \partial_{k} (\frac{h_{i} h_{j}}{h_{k}} \partial_{k} v)

即 :

\nabla^{2} = \frac{1}{| J |} \partial_{k} (\frac{h_{i} h_{j}}{h_{k}} \partial_{k}) (i, j, k 互 不 相 同, 对 k 求 和)

3.6.3 球坐标和柱坐标中 $\nabla$ 的表示：

根据上述讨论可以计算出球坐标和柱坐标中 $\nabla$ 的表示, 这里只写一下结果:

柱坐标

\begin{array}{l} \nabla = {(\partial_{r}, \frac{1}{r} \partial_{θ}, \partial_{z})}_{r, θ, z} \\ \nabla \cdot \vec{u} = \partial_{r} u_{r} + \frac{1}{r} (u_{r} + \partial_{θ} u_{θ}) + \partial_{z} u_{z} \\ \nabla \times \vec{u} = \frac{1}{r} | \begin{array}{c} {\vec{e}}_{r} & r {\vec{e}}_{θ} & {\vec{e}}_{z} \\ \partial_{r} & \partial_{θ} & \partial_{z} \\ u_{r} & r u_{θ} & u_{z} \end{array} | \\ \nabla^{2} u = \frac{1}{r} \partial_{r} (r \frac{\partial u}{\partial r}) + \frac{1}{r^{2}} \frac{\partial^{2} u}{\partial^{2} θ} + \frac{\partial^{2} u}{\partial^{2} z} \end{array}

球坐标

\begin{array}{l} \nabla = {(\partial_{r}, \frac{1}{r} \partial_{θ}, \frac{1}{r \sin θ} \partial_{φ})}_{r, θ, φ} \\ \nabla \cdot \vec{u} = \frac{1}{r^{2}} \partial_{r} (r^{2} u_{r}) + \frac{1}{r \sin θ} \partial_{θ} (\sin θ u_{θ}) + \frac{1}{r \sin θ} \partial_{φ} u_{φ} \\ \nabla \times \vec{u} = \frac{1}{r^{2} \sin θ} | \begin{array}{c} {\vec{e}}_{r} & r {\vec{e}}_{θ} & r \sin θ {\vec{e}}_{φ} \\ \partial_{r} & \partial_{θ} & \partial_{φ} \\ u_{r} & r u_{θ} & r \sin θ u_{φ} \end{array} | \\ \nabla^{2} u = \frac{1}{r^{2}} \partial_{r} (r^{2} \frac{\partial u}{\partial r}) + \frac{1}{r^{2} \sin θ} \frac{\partial}{\partial θ} (\sin θ \frac{\partial u}{\partial θ}) + \frac{1}{r^{2} \sin^{2} θ} \frac{\partial^{2} u}{\partial^{2} φ} \end{array}

ps. 以上只列出了矢量的梯度散度旋度运算，如果要是对张量，只作用于它的第一个角标即可。

3.7 张量运算的注意点

在直角坐标系中, 注意到偏微分符号作用于基矢为 $0$ , 即 $\partial_{i} {\vec{e}}_{j} = 0$ , 于是在直角坐标系中寻找基本公式会更加简单, 诸如前面提到的:

\begin{matrix} \nabla \cdot \nabla \times \vec{A} = 0 \\ \nabla f g = f \nabla g + g \nabla f \\ \nabla \cdot (f \vec{A}) = f \nabla \cdot \vec{A} + \vec{A} \cdot \nabla f \\ \nabla \times (f \vec{A}) = f \nabla \times \vec{A} + \nabla f \times \vec{A} \end{matrix}

的关系可以直接将其中的标量换为矢量, 只需要将上式的 $f, g$ 视为 $\vec{F}, \vec{G}$ 的一个分量即可:

\begin{matrix} \nabla \times \nabla \vec{F} = 0 \\ \nabla \vec{F} \vec{G} = \vec{F} \nabla \vec{G} + \vec{G} \nabla \vec{F} \\ \nabla \cdot (\vec{F} \vec{A}) = \vec{F} \nabla \cdot \vec{A} + \vec{A} \cdot \nabla \vec{F} \\ \nabla \times (\vec{F} \vec{A}) = \vec{F} \nabla \times \vec{A} + \nabla \vec{F} \times \vec{A} \end{matrix}

可以设想 $f = F_{i}, g = G_{j}$ , 再取上式的坐标分量, 那么就可以回到前面的结果. 由于矢量关系不随坐标系的选取而改变, 所以上式在任意曲线正交系都是成立的.

聪明的你或许已经发现, 将前面的方程向张量扩展, 我们要关注的其实只是 $\nabla$ 和张量基矢的关系. 对于梯度, 它不改变基矢量, 所以孤立的 $\nabla f$ 项直接替换为 $\nabla \vec{F}$ . 散度会作用于遇到的第一个基矢, 比如 $\nabla \cdot \vec{A} \vec{A} = \partial_{i} {\vec{e}}_{i} \cdot A_{j} {\vec{e}}_{j} A_{k} {\vec{e}}_{k} = \partial_{i} (A_{i} A_{k}) {\vec{e}}_{k}$ , 旋度也是同样作用于第一个遇到的基矢, 这会导致散度和旋度所作用的对象不能直接从标量或矢量替换为高阶的张量. 所以上面的后两个式子 $\nabla \cdot (\vec{F} \vec{A}) = \vec{F} \nabla \cdot \vec{A} + \vec{A} \cdot \nabla \vec{F}$ 和 $\nabla \times (\vec{F} \vec{A}) = \vec{F} \nabla \times \vec{A} + \nabla \vec{F} \times \vec{A}$ 是错误的. 实际的计算结果表明:

\begin{aligned} \nabla \cdot (\vec{F} \vec{A}) & = \partial_{i} (F_{i} \vec{A}) \\ = \vec{A} \partial_{i} F_{i} + F_{i} {\vec{e}}_{i} \cdot {\vec{e}}_{j} \partial_{j} \vec{A} \\ = \vec{A} \nabla \cdot \vec{F} + \vec{F} \cdot \nabla \vec{A} \end{aligned}

因为散度作用于张量 $\vec{F} \vec{A}$ 的左侧基矢, 并非像之前一样直接跳过 $f$ 而作用于 $\vec{A}$ 的基矢, 导致结果改变. 同样

\begin{aligned} \nabla \times (\vec{F} \vec{A}) & = ϵ_{i j k} \vec{e_{k}} \partial_{i} (F_{j} \vec{A}) \\ = \vec{A} \nabla \times \vec{F} + F_{j} ϵ_{i j k} \vec{e_{k}} \partial_{i} \vec{A} \\ = \vec{A} \nabla \times \vec{F} - \vec{F} \times \nabla \vec{A} \end{aligned}

不仅将 $\vec{F}, \vec{A}$ 调换, 还多出了一个负号.

3.8 物理人常用的矢量关系

罗列一下个人遇到的一些关系式, 待补充

3.8.1 关于位矢 $\vec{r}$

$\nabla \cdot \vec{r} = 3$ , $\nabla \vec{r} = I$ , $\nabla \times \vec{r} = 0$ , $I$ 是单位矢量
$\nabla r = \frac{\vec{r}}{r}$ , $\nabla \frac{1}{r} = - \frac{\vec{r}}{r^{3}}$
$\nabla^{2} (- \frac{1}{4 π r}) = \nabla (\frac{\vec{r}}{4 π r^{3}}) = δ^{3} (\vec{r})$
$\nabla \times f (r) \vec{r} = 0$

3.8.2 关于单位张量 $I$

$I : F = F$ , $F$ 是二阶及以上张量, $:$ 表示单位张量 $I$ 的两个指标都拿来做点乘
$I : \nabla \vec{B} = \nabla \cdot \vec{B}$
$\nabla \cdot φ I = \nabla φ$

3.8.3 其他

$\nabla B^{2} = \nabla (\vec{B} \cdot \vec{B}) = 2 \vec{B} \times (\nabla \times \vec{B}) + 2 \vec{B} \cdot \nabla \vec{B}$