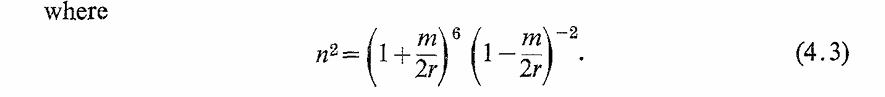1 hw-3 T-1 引力透镜

定义光程泛函 为:
其中 A、B 是光的起点和终点,费马原理指的是,所有连接 A、B 的可能曲线中,只有满足光程的变分为零才是光线走的路径,即:
在本题中,折射率是球对称的,光线始终在一个平面传播,可以采取极坐标:
代入拉格朗日方程 得到:
这是一个光学守恒量,记为 J,,称为光学角动量。在无穷远处, ,因为光线始终在一个平面传播,所以弧长微分满足:
代入 得到:
计算光线从无穷远来到近日点 ,再回到无穷远的总角度变化 ,有:
由 ,可得:
使用变量代换 ,则 ,于是:
代入 ,化为:
注意,最终的偏折角是 ,减去 是因为在没有引力时,偏折角是 而不是 0。所以偏折角:
2 hw-5 T-3 电荷在电磁场中运动的对称性

(a)
直接代入(3)到(1)得到拉氏量在 boost 下不变:
为了找到守恒荷,可以将无限小 boost 视为一种平移,即取 :
也即
于是守恒荷是:
对应的守恒量就是 。
假设有多个粒子,将 x 选取为系统质心的坐标,在题示拉氏量所表示的自由运动下,,于是守恒量 ,恰好前后相容,即系统的惯性中心保持匀速运动(更一般的,我们常说这个守恒量反映能量中心保持匀速运动,因为 ),这个守恒量其实没什么意思。
(b)
同理,根据 ,已经知道 在 boost 下不变,所以只需考虑 ,这里 而不是为 0,是因为题目要求让作用量不变,而不是让拉氏量不变:
即
这是一个全微分,所以需要满足:
即
注意到 2 维时空中 ,上式变为:
这是一个一阶线性齐次偏微分方程,可以使用特征线法来求解这个方程,特征线的微分方程为:
沿着特征线可知 在特征线上是常数,所以 必须满足:
即电场本身就是洛伦兹不变的,特征线就是世界线 。
注意,加入电磁场后,广义动量变为
于是守恒荷是:
3 hw-6 T-3

在势能 上增加一个小的修正 , 有限运动的轨道不再封闭, 并且每运动一圈轨道的近心点都有很小的角度改变量 。在下面的情况下求 : a) , b) .
解:根据公式 , 当 从 变到 再变到 时, 角变量 的变化量 , 也即相邻近心点对力心的夹角为
将 代入上式, 注意到 为小量, 可以对上式中的被积函数作 Taylor 展开, 并保留到 的一阶项, 有
由此式 变为
其中第一项对应于在势能为 的场中质点运动轨道的相邻近心点对力心的夹角, 它等于 。上式中的第二项是势场修正引起的角变量的变化, 记为 , 即
利用力场未受修正时 与 之间的关系 (参见式 )
则式 可以改写为
a) 当 时, 则有
于是由式 可得
对于这种情况, 势能实际上为
另外,质点在该力场中的运动是可以解析求解的。为此我们采用 Binet 公式 求解, 用 表示时, 有
即
这个方程的解为齐次方程的通解和非齐次方程的特解之和, 即
其中 为积分常数, 这里选取合适的初始条件使得初位相为零, 由上式, 可得
其中
由式 可知, 轨道是有限的, 但是, 当 从 变到 时, 从其极小值 变到 ; 不回到初始的位置, 即轨道不封闭.
从式 可知, 相邻两个近心点 (或远心点) 之间的夹角 满足关系
即
当对力场没有修正, 即 时, 这个夹角应为 。可见为力势的变化导致近心角的改变为
其中最后一个等号是假定 为小量的结果, 这与式 是相同的。
b) 当 时, 有
其中 , 将其代入式 可得
在这种情况下, 势能为
相应地, 有心力为
其中第二项可以视为广义相对论对万有引力 (第一项) 的修正, 由此可以解释水星近日点的进动问题。在经典力学中该力场相关轨道的求解以及运动性质的讨论可参考有关文献。
ps:本题用拉格朗日方程/运动方程 + 微扰也可以求解
4 hw-6 T-5 选做题
4.1 (a)
选取坐标参数如下:
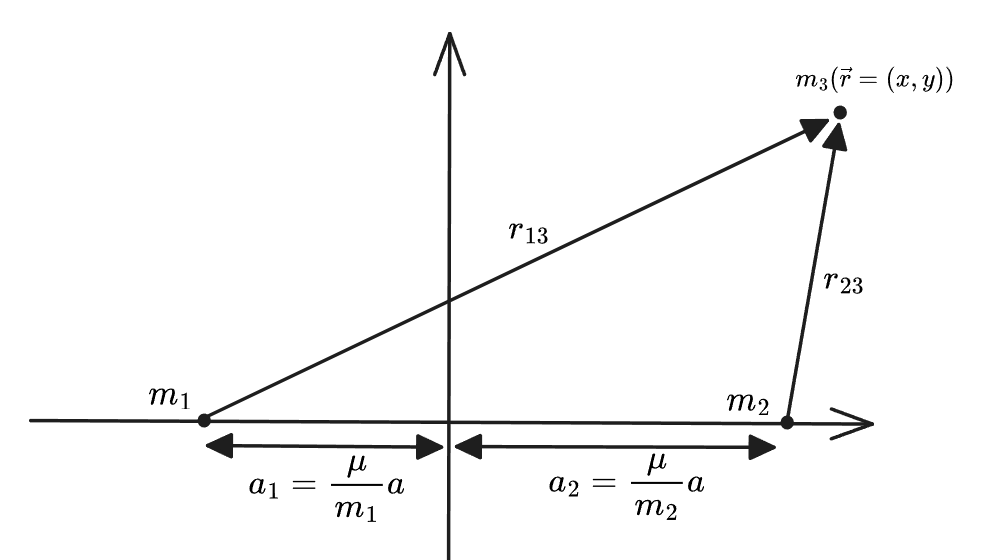
在静止系中的速度是
于是拉氏量是
代入拉格朗日方程得到 的运动方程:
显然上式第二项就是科里奥利力。对于平衡点,要求 ,即上式左侧为 0,即
i) 若 ,(2)就意味着:
代入(1)消去 或 就得到:
与 对比可知
也就是 构成等边三角形,对应的解就是下图的 和 。
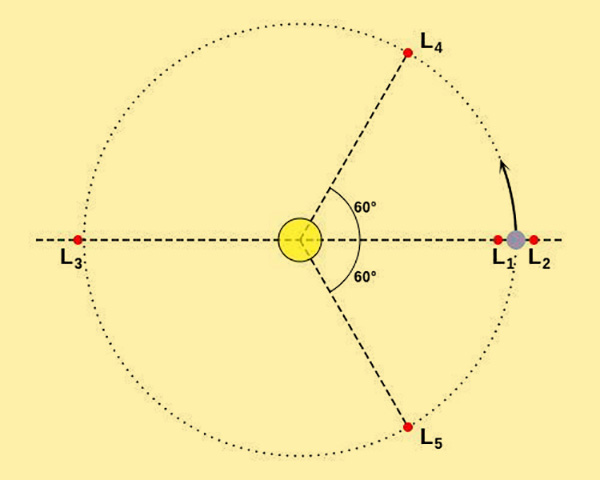
ii) 若 ,(1)式就简化为
该方程没有解析解,只能用数值方法去逼近,它有三个解,对应于上图的 。当然,在限制性三体问题中 ,上式有近似解,就比如常见的日-地-月三者,就构成一个这样的限制性三体系统。
4.2 (b)
这道题没有给定参数的具体值,所以同学们可以任取(比如 )。这里就以地-月-卫星系统为例,因为它是限制性三体系统,所以
对应的绘图如下:
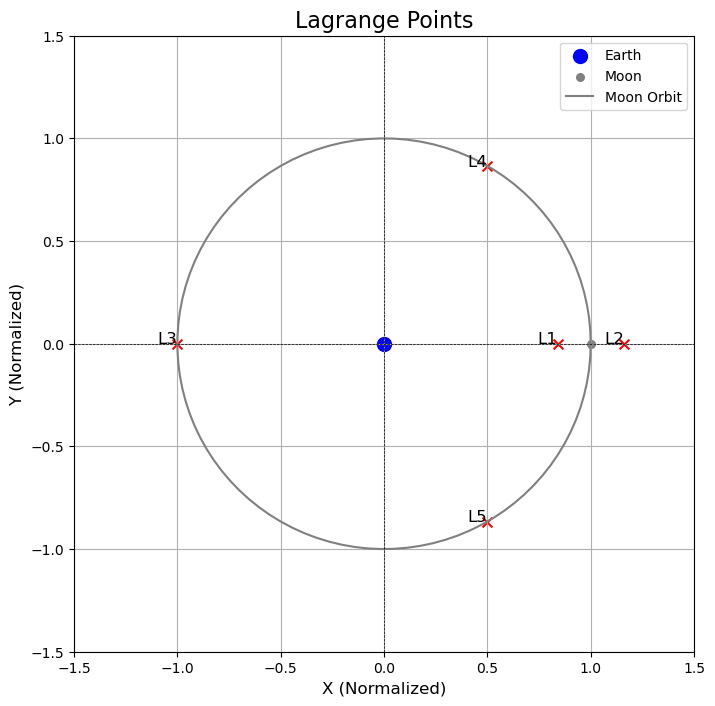
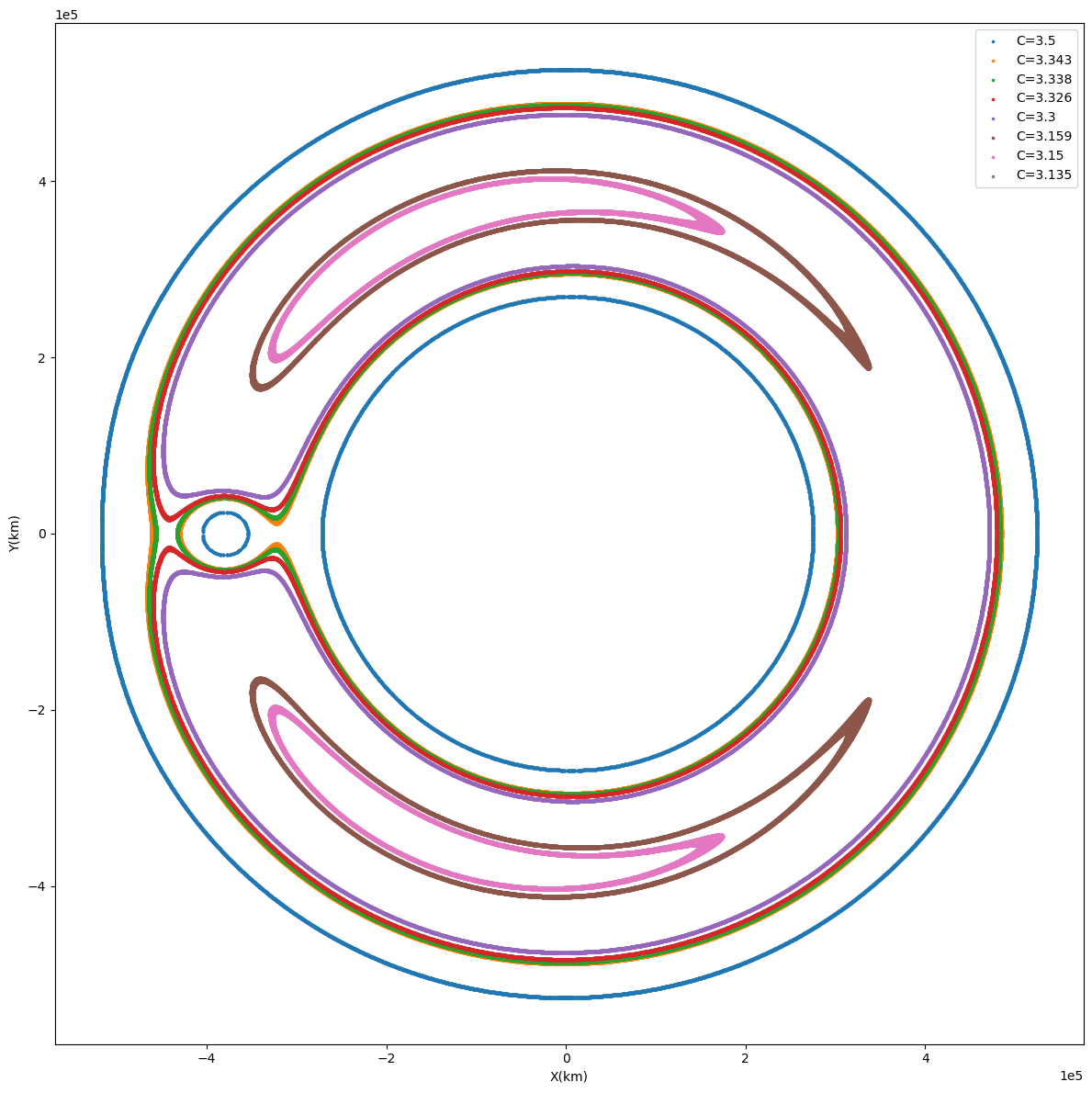
至于题目中的等势面,描述的其实就是相对于旋转系的速度为 0 的零速度面,我们一般称之为 Hill 曲面。它对应的表达式是(这里还是采用和第一问一样的,以质心为原点,而不是题目中以 为原点):
绘制这个图对 C 的精度要求比较高,画出来是
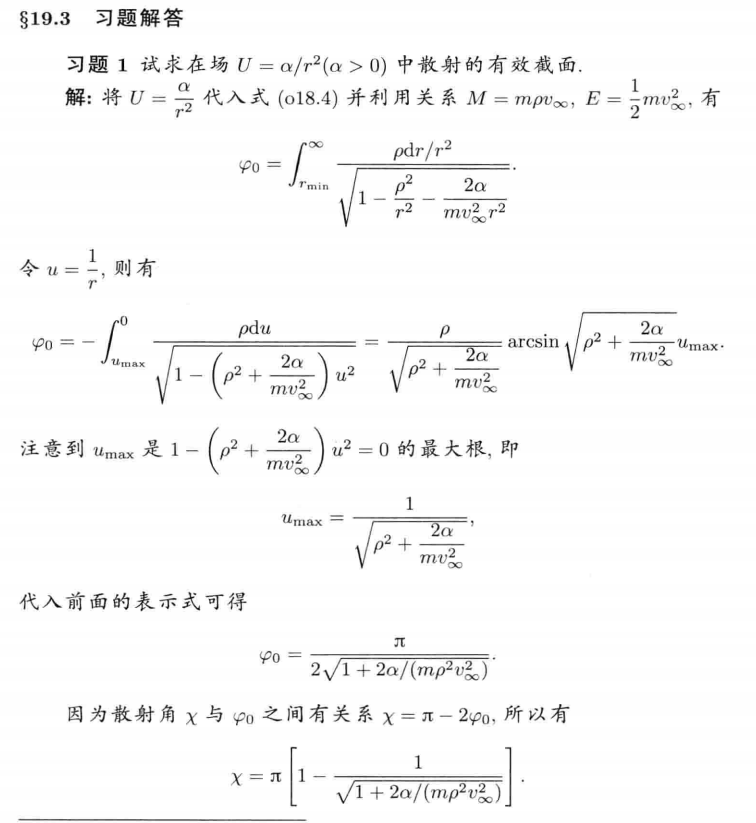
5 散射


draft:其他想法
- Curvilinear Coordinate
- Vector/Tensor Algebra
- Lie Group
- Others