Answer for HW6
前三题的解析是鞠国兴解读的教材原内容。注意,它采用了一个奇怪的记号,即用 M 来表示角动量。
1 T1~T3:有心力场
1.1 前情提要
如果作用在质点上的力的方向总是沿着质点的径矢,这样的力称为有心力。如果该力的大小仅仅与质点到固定点的距离有关,则有
在有心力场中,质点的运动位于一个固定平面内,该平面垂直于角动量
坐标
运动的轨道方程为
其中
称为有效势能,而
根据转折点以及质点的运动范围, 可以分为有界运动和无界运动。有界运动通常有两个转折点。
对于
等于
质点可以坠落至场中心, 即
1.2 T1
质点在场
解:本题要求抛物线轨道相应的参数方程。由式
作变量代换
其实也可以直接利用积分公式
作前述的变量变换可得与前面相同的结果。因为
利用关系
注意,因为
1.3 T2
质点在有心力场
解:将函数代入式
这给出了
为求
积分的结果取决于参数的取不同值, 可以分为几种情况.
a) 当
即
当
即
这种情况下的典型轨道是螺线, 常称为 Cotes 螺线。图例:
r = \sec(0.05 \theta + 1)|0<\theta< 10
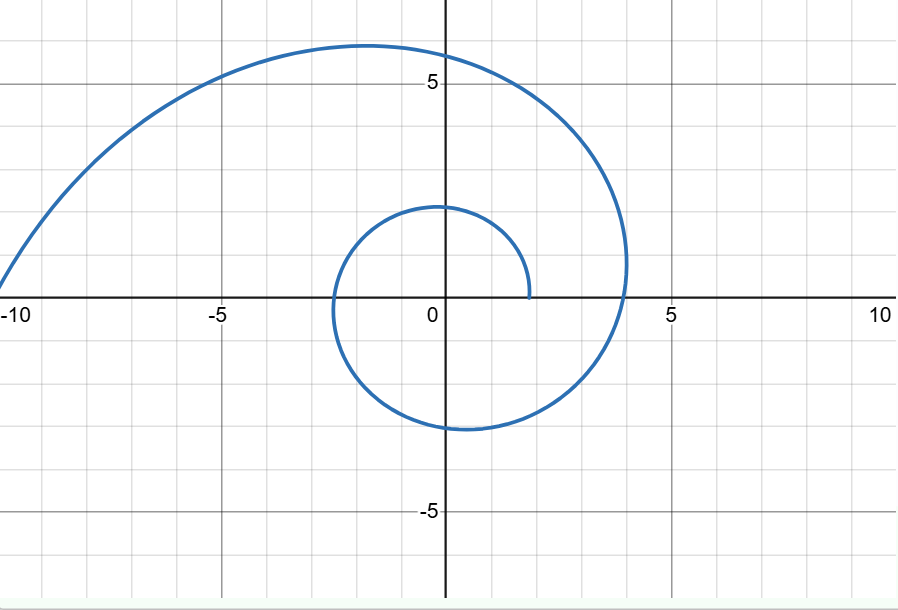
b) 当
即
同样
c) 当
即有
当
即
需要说明的是:
- (i)
, 这种情况需要排除, 因为这将导致复数的 . - (ii) 在 b) 和 c) 两种情况下, 当
时, 均有 , 即质点可以“坠落”到力心. - (iii) 本问题用 Binet 公式可以比较方便的求解, 参见本节 T3.
本问题中质点的运动特征也可以通过有效势能进行分析. 有效势能为
当
这与式
1.4 T3
在势能
解:根据公式
将
由此式
其中第一项对应于在势能为
利用力场未受修正时
则式
a) 当
于是由式
对于这种情况, 势能实际上为
另外,质点在该力场中的运动是可以解析求解的。为此我们采用 Binet 公式
即
这个方程的解为齐次方程的通解和非齐次方程的特解之和, 即
其中
其中
由式
从式
即
当对力场没有修正,即
其中最后一个等号是假定
b) 当
其中
在这种情况下, 势能为
相应地, 有心力为
其中第二项可以视为广义相对论对万有引力 (第一项) 的修正, 由此可以解释水星近日点的进动问题。在经典力学中该力场相关轨道的求解以及运动性质的讨论可参考有关文献。
2 T4
记
其中
代入(1)式可得到:
右侧第一项是常矢量,且由于
3 T5: 选做题
3.1 (a)
选取坐标参数如下:
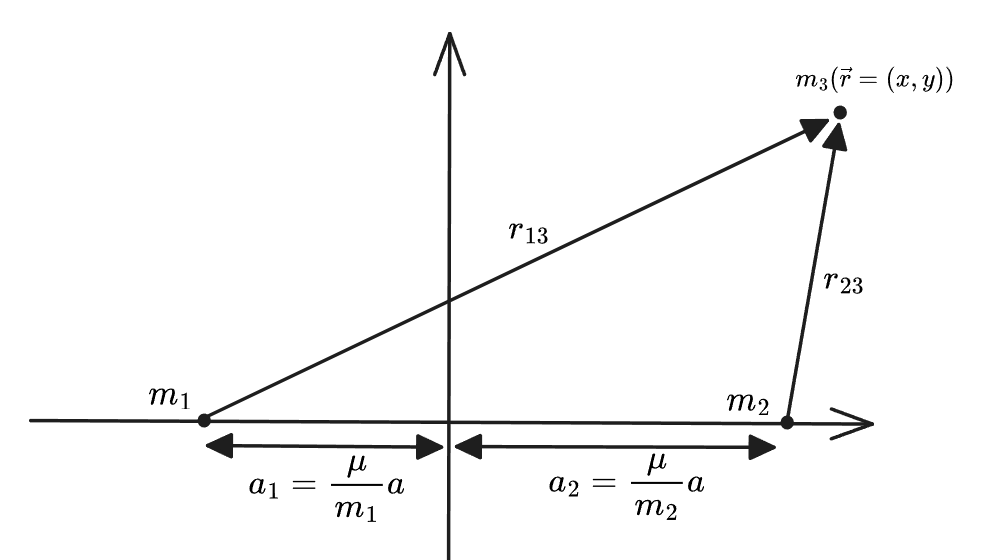
于是拉氏量是
代入拉格朗日方程得到
显然上式第二项就是科里奥利力。对于平衡点,要求
i) 若
代入(1)消去
与
也就是
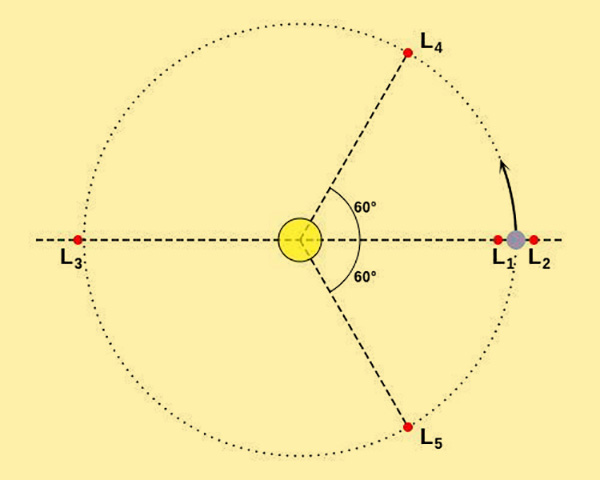
ii) 若
该方程没有解析解,只能用数值方法去逼近,它有三个解,对应于上图的
3.2 (b)
这道题没有给定参数的具体值,所以同学们可以任取(比如
对应的绘图如下:
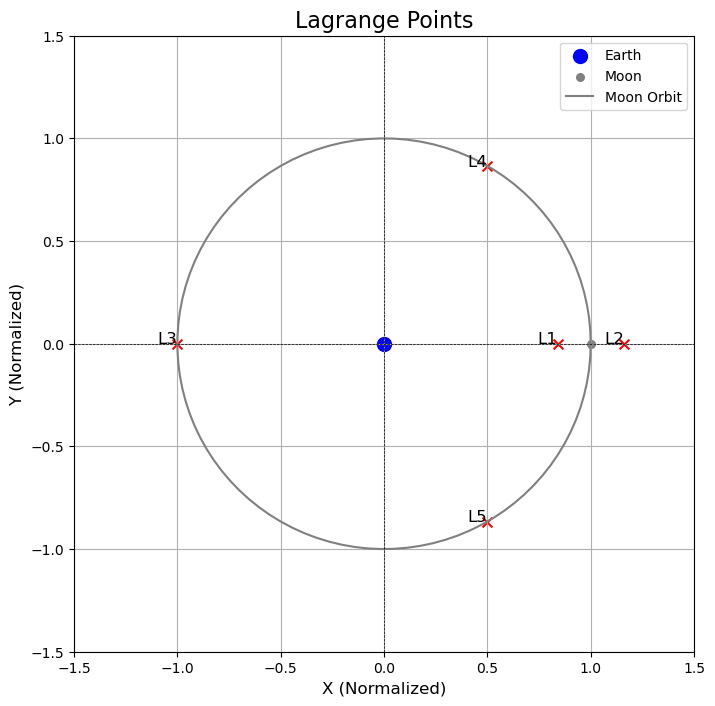
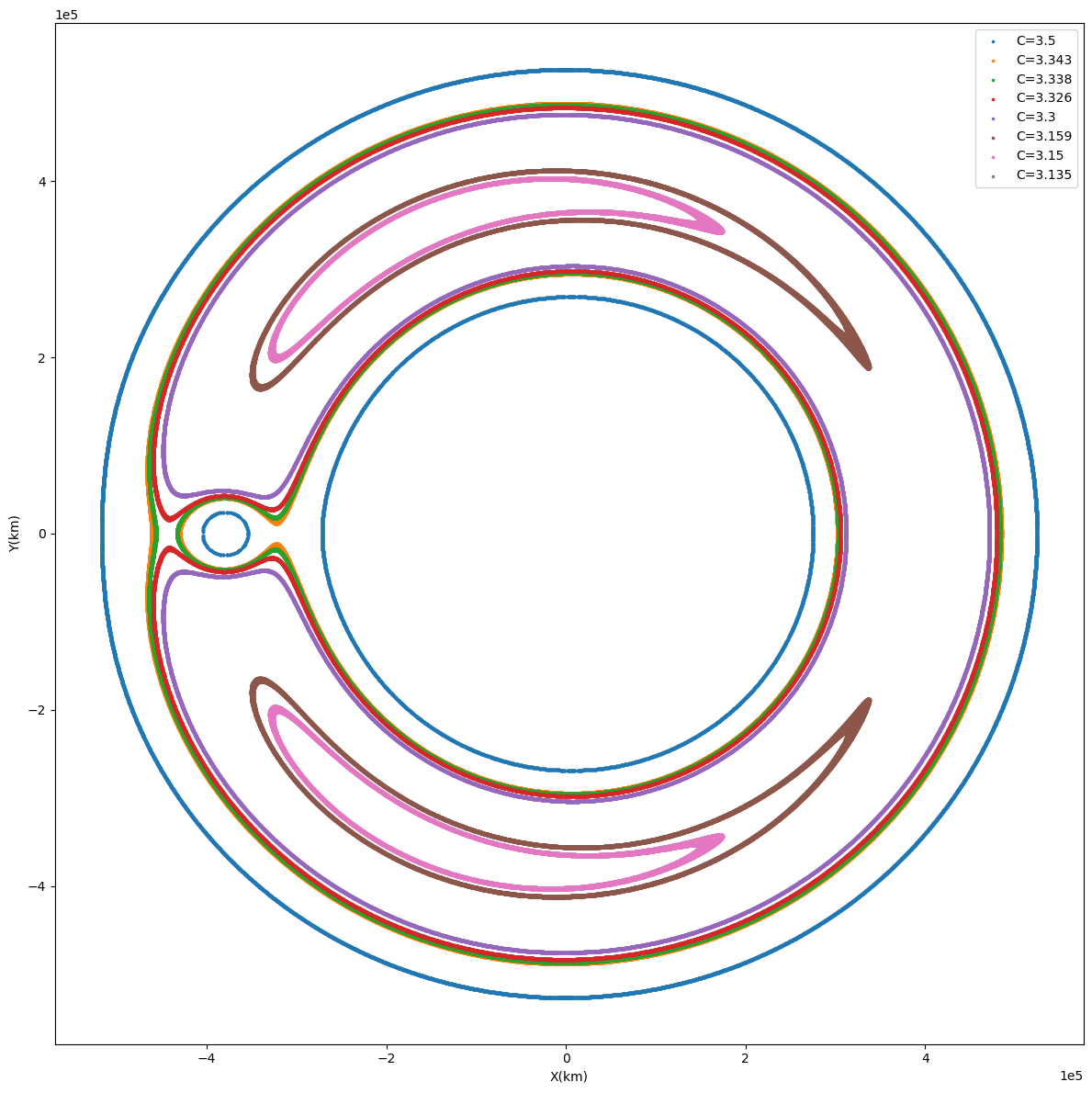
至于题目中的等势面,描述的其实就是相对于旋转系的速度为 0 的零速度面,我们一般称之为 Hill 曲面。它对应的表达式是(这里还是采用和第一问一样的,以质心为原点,而不是题目中以
绘制这个图对 C 的精度要求比较高,画出来是
Appendix 代码 %
上面两幅图用 python 绘制,代码是
# 绘制拉格朗日点
import numpy as np
import matplotlib.pyplot as plt
# 相对质量
earth_mass = 1.0
moon_mass = 7.342e22/(5.972e24)
R = 1.0 # 地月距离(归一化)
earth_position = np.array([0.0, 0.0])
moon_position = np.array([R, 0.0])
lagrange_points = [
{"name": "L1", "position": np.array([0.84, 0.0])},
{"name": "L2", "position": np.array([1.16, 0.0])},
{"name": "L3", "position": np.array([-1.0, 0.0])},
{"name": "L4", "position": np.array([0.5, np.sqrt(3)/2])},
{"name": "L5", "position": np.array([0.5, -np.sqrt(3)/2])},
]
plt.figure(figsize=(8, 8))
plt.scatter(earth_position[0], earth_position[1], color='blue', s=100, label='Earth')
plt.scatter(moon_position[0], moon_position[1], color='gray', s=30, label='Moon')
for point in lagrange_points:
plt.scatter(point["position"][0], point["position"][1], color='red', marker='x', s=50)
plt.text(point["position"][0], point["position"][1], point["name"], fontsize=12, ha='right')
# 绘制月球轨道
theta = np.linspace(0, 2*np.pi, 100)
r = R * np.ones_like(theta)
plt.plot(r * np.cos(theta), r * np.sin(theta), color='gray', linestyle='-', label='Moon Orbit') # ecc=0.055忽略
plt.title('Lagrange Points', fontsize=16)
plt.xlabel('X (Normalized)', fontsize=12)
plt.ylabel('Y (Normalized)', fontsize=12)
plt.legend()
plt.grid(True)
plt.axhline(0, color='black', linewidth=0.5, linestyle='--')
plt.axvline(0, color='black', linewidth=0.5, linestyle='--')
plt.xlim(-1.5, 1.5)
plt.ylim(-1.5, 1.5)
plt.show()
# 绘制希尔曲线族
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
G = 6.6743e-11 # m^3 kg^-1 s^-2
M = 5.972e24 # kg
m = 7.342e22 # kg
mu_1 = 398600 # km^3/s^2
mu_2 = 4903.02 # km^3/s^2
R = 3.844e5 # km
omega = np.sqrt((mu_1 + mu_2) / (R**3)) # 月球绕地球的角速度
# 网格
x = np.linspace(-6e5, 6e5, 20000)
y = np.linspace(-6e5, 6e5, 20000)
z = np.array([0])
x, y, z = np.meshgrid(x, y, z, indexing='ij')
earth_x = (m / (M + m)) * R # 假设地月质心在原点
moon_x = -(M / (M + m)) * R
# spacecraft 到地球和月球的距离
r_e = np.sqrt((x - earth_x)**2 + (y)**2 + (z)**2)
r_m = np.sqrt((x - moon_x)**2 + (y)**2 + (z)**2)
C_jacobi = 2 * mu_1 / r_e + 2 * mu_2 / r_m + omega**2 * (x**2 + y**2) # 计算势能
def plot(C, ax):
# 绘制希尔曲面
mask = (C_jacobi < C) & (C_jacobi > C-0.001)
print(f"num of points: {np.sum(mask)}")
ax.scatter(x[mask], y[mask], marker='.', s=10, alpha=1, label=f"C={C}")
# 设置坐标轴标签等
ax.set_xlabel('X(km)')
ax.set_ylabel('Y(km)')
ax.ticklabel_format(style='sci', scilimits=(0,0), axis='both')
fig, ax = plt.subplots(figsize=(12, 12))
for i, C in enumerate([3.500, 3.343, 3.338, 3.326, 3.300, 3.159, 3.150, 3.135]):
print(f"C={C}")
plot(C, ax=ax)
plt.legend()
# plt.tight_layout()
plt.show()